Matematika SMA

Invers dan Determinan Matriks

Sholihin 5 November 2011 25 Comments
Matriks 3x3
Matriks 3×3

Mencoba memenuhi permintaan dari sobat Bryan untuk posting tentang invers dan determinan matriks, maka pada postingan kali ini akan mencoba membahas sedikit materi yang berkaitan dengan invers dan determinan matriks.

Matriks merupakan susunan bilangan-bilangan berbentuk persegi atau persegi panjang yang diatur menurut baris dan kolom tertentu. Matriks dinotasikan dengan huruf kapital. Jika m adalah banyaknya baris dari matriks A, dan n adalah banyaknya kolom dari matriks A, maka matriks A mempunyai ordo m \times n, atau ditulis A_{m\times n}.

A_{m \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}

1. Invers Matriks

Jika A dan B adalah matriks persegi, dan berlaku A \cdot B = B \cdot A = I maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis A^{-1}. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
Jika A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} dengan ad - bc \neq 0, maka invers dari matriks A (ditulis A^{-1}) adalah sebagai berikut:

A^{-1} = \frac {1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}

Jika ad - bc = 0 maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.

Sifat-sifat matriks persegi yang mempunyai invers:

  • (A \cdot B)^{-1} = B^{-1} \cdot A^{-1}
  • (B \cdot A)^{-1} = A^{-1} \cdot B^{-1}
  • (A^{-1})^t =(A^{t})^{-1}

Contoh: Tentukan invers dari matriks berikut!

\begin {array} {lcl} A & = & \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \\ A^{-1} & = & \frac {1}{2 \times 3 - 1 \times 5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{6-5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{1} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ A^{-1} & = & \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix}\end{array}

2. Determinan Matriks

Syarat suatu matriks dapat dicari determinannya adalah matriks tersebut harus merupakan matriks persegi. Jika A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, maka rumus untuk mencari determinan matriks berordo 2×2:

det A = \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc

Sedangkan untuk mencari determinan matriks berordo 3×3 menggunakan aturan Sarrus.

A_{3 \times 3} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}

\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix}

\begin{array} {lcl} \begin{vmatrix} A \end{vmatrix} = && a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ & - & a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{array}

Contoh: Tentukan determinan dari matriks berikut!

A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \end{bmatrix}

\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 5 & 2 \end{vmatrix} = 3 \times 2 - 1 \times 5 = 6 - 5 = 1

B = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{bmatrix}

\begin{vmatrix} B \end{vmatrix} = \begin{vmatrix}1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{vmatrix} \begin{matrix} 1 & 2\\ 1 & 3 \\ 1 & 4 \end{matrix}

\begin{array} {lcl} \begin{vmatrix} B \end{vmatrix} & = & 1.3.3 + 2.4.1 + 3.1.4 - 1.3.3 - 4.4.1 - 3.1.2 \\ & = & 9 + 8 + 12 - 9 - 16 - 6 \\ & = & -2 \end{array}

 

25 Replies to “Invers dan Determinan Matriks”

  3. aku mau nanya nih, bisa apa ngak ya… postingan di atas kan di tulis yg bisa dicari dterminannya matriks persegi.
    trus ada tidak determinan matriks yang ber-ordo 4 x 4, 5×5,6×6…..???
    trus low ada cara cari determinannya gimana??
    thanks

    Balas

    1. Yups, bener banget. Yang bisa dicari determinannya hanya matriks persegi.
      Untuk matriks persegi 4×4, 5×5, 6×6 tentu saja bisa dicari determinannya, tetapi caranya berbeda dengan cara mencari determinan matriks 2×2 dan 3×3. Untuk mencarinya bisa menggunakan sifat-sifat determinan, aturan permutasi, atau bisa juga dengan menggunakan kofaktor.
      🙂

      Balas

    1. Thank you, I don’t have special tips, but you can try to keep nice post 🙂
      thank’s for your attention and this is only on my mind and i try to repair, and repair my blog. Let’s join with this blog and you’ll find many advantages from my blog especially about mathematics.

      Balas

    1. Transpose suatu matriks, misal matriks A, ditulis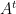 A^t didapat dengan mengubah elemen-elemen matriks pada baris ke-1 menjadi kolom ke-j, begitu sebaliknya.
      Contoh
      A = \begin{bmatrix} 1 & 2 \\ 3 & 4\\ 5 & 6 \end{bmatrix}
      Maka
      A^t = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}
      Apakah sudah jelas?

      Balas

    1. Untuk materi ajar PPL artikel di atas bisa dicopy paste di microsoft word, gunakan browser chrome, opera atau internet eksplorer. Tetapi persamaan matematika yang ada tidak bisa diedit di word, karena itu khusus untuk web, gantinya persamaan matematika tersebut bisa disave sebaga gambar.

      Balas

  9. dari sekian banyak situs pembelajaran matematika, yang lebih terasa blognya mas ini, saya berterima kasih banyak karena sudah banyak membantu saya karena “bahasa”nya mudah saya pahami 😀

    oh ya, ada masukan dari saya:
    -jika berkenan, tiap materi diberi cara cepat
    -diberi konten swf (flash) karena cara belajar saya lebih cenderung ke visual 🙂 hehe

    trims

    Balas

    1. Trimakasih masukannya mas,
      untuk materi yang saya sampaikan sebisa mungkin saya menyampaikan konsep dahuli, agar lebih paham. Untuk cara cepat menurut saya akan lebih efektif kalau konsepnya sudah benar-benar paham, sehingga cara cepat bisa dijadikan alternatif.
      Kontent .swf atau flash juga saya pernah menggunakannya, misal pada postingan vektor posisi suatu titik. Tetapi karena memberatkan blog dan juga mengurangi bandwith hosting, maka saya copot, tapi masih bisa melihat file swf tersebut dengan cara mendownloadnya terlebih dahulu.
      Sekali lagi trimakasih masukannya.

      Balas

    1. Silakan, kalau mau di republish diusahakan disertakan sumbernya juga ya. Trus jangan sama persis, biar tidak dianggap duplikat kontent ma om Google.
      Kalau untuk konsumsi pribadi, silakan 🙂

      Balas
  11. Ping-balik: URL
  13. Ping-balik: LAPORAN WORKSHOP PEMBELAJARAN MATEMATIKA « febriliaanjarsari

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *