Dari komentar Pak Wandi pada postingan soal dan pembahasan bilangan ke-1439, beliau mengajukan beberapa soal lagi. Mungkin masih berkaitan dengan soal PASIAD 2010, karena tidak disebutkan sumber soalnya. Jika dari pembaca sekalian ada yang mengetahuinya, dimohon agar memberitahukan lewat komentar agar bisa ditambahkan informasi sumber soal. Soalnya kurang lebih seperti ini:
- Tentukan
- Tentukan nilai x jika (2^x-4)^3+(4^x-2)^3=(4^x+2^x-6)^3==> x=? [Jujur saja penulisan bentuk soal tersebut agak rancu, bisa berarti
atau
karena saya belum bisa sepenuhnya memahami soal yang dimaksud dan belum mendapat konfirmasi soal yang benar bagaimana].
Jawab:
1. Untuk menjawab soal pertama, lakukan manipulasi bentuk aljabar tersebut.
Dari bentuk tersebut, maka bentuk umumnya adalah untuk
maka:
Jawaban tersebut masih bisa disederhanakan, tinggal disesuaikan dengan pilihan jawaban kalau ada.
2. Ini maksud soalnya saya kurang paham, apakah atau
Untuk melihat soal yang dimaksud, silakan menuju komentar Pak Wandi.
Menurut komentar mas Tutur, soal nomor 2 cenderung ke bentuk soal , dan beliau juga memberikan jawabannya sebagai berikut:
Misalkan, dan
maka soal menjadi equivalen dengan bentuk
Karena maka diperoleh,
Substitusikan kembali nilai a dan b, diperoleh
Untuk , maka
Untuk , maka diperoleh
Untuk , tidak ada nilai x yang memenuhi.
Untuk , diperoleh
Jadi,
[Diperbaharui, Senin 12 Maret 2012]
Kiranya sekian dahulu contoh pembahasan soal olimpiade matematika SMP, mohon koreksinya misal terdapat kesalahan. Jika ada pertanyaan atau ada yang masih kurang jelas silakan ajukan lewat komentar. Terimakasih.

Untuk komentar disini aja udah harus belajar matematika. 0 + 8 = ?????
Untuk mencegah spam mas, makanya dipasang pake quis kaya gitu. Mengurangi penggunaan plugin 🙂
Halo Pak Wandi, udah dijawab nih soalnya,hehe Mantap sekali mas penjelasannya,hehe
Iya nih Pak Wandi belum konfirm lagi soal yang nomer 2, lagi ngurus anekaberita mungkin mas xixixi
hehe., makin butek aja nih otak lihat angka2 tersebut., aku cuma lancar klo lihat angka 5000+1000=6000 😀
taluk mas ah
Kalo ngliat angka earning dolar gak mbulet ya mas? hahaha 😆
Untuk menuliskan notasi matematika memang harus jelas, khususnya soal No. 2
Itulah knapa jika mendikte soal ke siswa, kayaknya nggak cukup dan musti harus disertai tulisannya.
Seberapa banyak tanda kurung juga bisa amat menentukan maksud soal.
Misalnya saya mendike “dua pangkat x dikurangi 5, meski sudah pakai intonasi yg benar, tapi bukan tak mungkin masih ada yg salah tulis.
Ada yg mengira (2^x) – 5 dan ada yang berpikir 2^(x-5)
Iya Pak, betul sekali. Karena persepsi dan daya tangkap siswa bisa berbeda, maka penulisan di papan tulis menjadi alternatif yang bisa mengurangi tingkat kesalahan siswa dalam menuliskan soal.
Saya ada soal sederhana yang belum jelas sampai sekarang
[(-1)^2]^(1/2) itu jawabnya -1; 1 atau plus minus 1 Mas?
Atau malah bukan semuanya???
Mudah2an bisa dijelaskan disini
Untuk Pak Wandi juga boleh ikut njawab soal saya 😀
Kalo soal saya ini sich bukan soal Olimpiade juga bukan dari Pasiad.
Ini soal biasa, soal eksponen kelas X SMA…
Dan bilangannyapun nggak yang ribuan, nggak faktorial
Masih <10 😀
Berarti soalnya![[(-1)^2]^\frac{1}{2} [(-1)^2]^\frac{1}{2}](https://s0.wp.com/latex.php?latex=%5B%28-1%29%5E2%5D%5E%5Cfrac%7B1%7D%7B2%7D&bg=ffffff&fg=000000&s=0) ya pak?
ya pak?
![[(-1)^2]^\frac{1}{2}=(-1)^1=-1 [(-1)^2]^\frac{1}{2}=(-1)^1=-1](https://s0.wp.com/latex.php?latex=%5B%28-1%29%5E2%5D%5E%5Cfrac%7B1%7D%7B2%7D%3D%28-1%29%5E1%3D-1&bg=ffffff&fg=000000&s=0) atau
atau
![[(-1)^2]^\frac{1}{2}=[1]^\frac{1}{2}=\sqrt{1}=1 [(-1)^2]^\frac{1}{2}=[1]^\frac{1}{2}=\sqrt{1}=1](https://s0.wp.com/latex.php?latex=%5B%28-1%29%5E2%5D%5E%5Cfrac%7B1%7D%7B2%7D%3D%5B1%5D%5E%5Cfrac%7B1%7D%7B2%7D%3D%5Csqrt%7B1%7D%3D1&bg=ffffff&fg=000000&s=0)
Saya juga pernah menemui hal seperti itu pak, Kalau menurutku
Jadi jawabannya 1 atau -1.
CMIIW
Nah disitu masalahnya Mas…
Kalau ada siswa yg hanya ngerjakan salah satu trus dibenarkan apa disalahkan>. Karena kalau jawabnya 1 atau -1 kok cuma dijawab salah satu kan termasuk salah (inilah prinsip Matematika yg kadang nggak bisa diterima awam.
Sama seperti kasus x^2 = 9, x=…
Kalau dijawab 3 saja kan salah.
Karena menggunakan kata penghubung atau maka kalau ada yang menjawab salah satu dibenarkan saja pak 🙂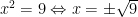
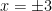
Benar juga pak,
Maka
Haruskah disalahkan kalau hanya menjawab 3? Saya rasa tidak harus sampai disalahkan pak 🙂
Saya amat sangat bingung ketika anak mengerjakan hanya sampai ketemu -1 terus berhenti, harus saya benarkan atau saya anggap salah
(Matematika kan nggak kenal perikemanusiaan)
Tapi kalau saya salahkan kok ya nggak pas, karena anak tersebut sudah secara benar mengamalkan rumus (a^m)^n adalah a^(mn)
Dan pemakaian kata hubung “atau” sepengetahuan saya bukan seperti itu, kecuali kalau semestanya logika matematika.
Memang benar kalau “atau” itu cukup salah satu benar, tapi tidak bisa untuk memberi toleransi manakala menjawab x^2=9 trus x=-3… 😀
CMIIW juga
Di matematika tak kenal kurang sedikit atau lebih sedikit, apalagi cuma separo.
kalau jawabnya 3 dan -3 kok hanya dijawab 3, itu maknanya jawabannya baru separo. Tingkat salahnya sama ketika njawab 4 X 25 dijawab 50, karena baru separo juga
Ya mungkin perlu dijelaskan kepada siswa sejak awal pak, kalo menjawab soal seperti itu harus dua-duanya sekalian saja, biar disiplin 🙂
Mungkin link ini bisa membantu menjawab pak, monggo silakan 🙂
http://www.wolframalpha.com/ trus pada kolom input coba masukkan ((-1)^2)^0.5
numpang mampir pak.
Maaf saya tidak setuju kalo jawaban soal di atas adalah 1 atau -1.
Menurut saya jawabnya adalah 1.
Yang perlu diperhatikan adalah untuk setiap bilangan riil x berlaku (x^2)^(1/2)=|x|.
Jadi, harus hati – hati menggunakan aturan pangkat untuk bilangan negatif. Andaikan kita boleh menjawab
[(-1)^2]^(1/2)=(-1)^1= -1
maka coba perhatikan bukti di bawah ini :
-1=(-1)^1=[(-1)^2]^(1/2)=1^(1/2)=1
yang jelas salah.
Demikian juga bila, [(-1)^2]^(1/2)= -1 maka kita juga bisa membuktikan bahwa -3=3, -4=4, dst.
Trimaksih masukannya mas, memang kalau berdasarkan konsep nilai mutlak jawabannya adalah 1.
Diskusi di atas mencoba melihat permasalahan tersebut berdasarkan sifat-sifat perpangkatan, yang jujur saja saya juga kadang masih bingung dengan jenis soal yang menjebak seperti itu 🙂
wah, baru menemukan blog ini dari halamannya mba Nique…
salam kenal dulu nih sama pak tutornya… 🙂
anakku pasti akan senang dan akan bolak balik hadir di rumah mayamu nih mas…
thanks for the pages yaaa….
Iya bu, salam kenal juga.
Senang kalo tulisannya bisa bermanfaat dan bisa membantu yang lain 🙂
PASIAD tu apa ya mas?? maaf saya baru dengar…
Setauku PASIAD merupakan yayasan Asosiasi Solidaritas Sosial untuk Negara-negara Pasifik dari Turki, ada juga PASIAD Indonesia, salah satu kegiatannya ya mengadakan kompetisi matematika.
CMIIW
your post is nice.. 🙂
keep share yaa, ^^
di tunggu postingan-postingan yang lainnya..
jangan lupa juga kunjungi website dunia bola kami..
terima kasih.. 🙂
wah mumet saya liat angka-angka diatas 😀
Jangan cuma dilihat mas Andank, tapi dipahami biar gak mumet 🙂
OOT, sepertinya DOCTYPE-nya perlu disesuaikan.
Selebihnya coba memahami, walaupun rada-rada mumet 😀
Doctype-nya perlu disesuaikan gimana pak? saya tidak mudeng hee….
dulu waktu sd juara matematika se kecamatan 😀
sekarang fusing lihat gituan,
klo ngitung 2% kali 1 em gitu masih bisalah…. xixixi…
Wah hebat donk mas, bisa juara se kecamatan. Dulu saya pas SD belum pernah diikutkan lomba matematika, cuma pas SMA thok.
wa baru tau ni ada blog Matematika SIP lah mantab
izin save
Monggo silakan saja di save, moga bermanfaat.
aku suka ini Pak, dan saya tunggu jawaban yang kedua, mohon beritahu ya klo sudah di post
Trimakasih Pak, ini soal yang kedua masih menunggu konfirmasi dari pemberi soal, silakan sering-sering mampir Pak. Atau silakan berlangganan artikel via email, cukup masukkan alamat email dan klik OK pada sidebar kanan, dan konfirmasi email lewat inbox.
Untuk jawaban soal nomer dua sudah saya perbaharui pak, silakan dicek jawaban di atas.
ediaan tenan 😀
saya paling kurang menyukai matematika mas 😀
btw syaa liat page view masing2 postingan banyak banget.. maknyoooss
Saya lebih suka pelajaran eksak daripada hafalan macam IPS, PPKn dan sebangsanya 😀
Kalau menurutku view postingannya kurang valid mas, soalnya kalau gak salah misal kita buka homepage, maka postingan yang ada dihomepage juga ikut nambah, atau misal kita edit suatu postingan dan kita lihat perubahannya juga nambah. Tapi ya moga aja memang banyak yang membaca postingannya 🙂
wah, ada deret matematika. hehe. deret apa mas itu? ganjil apa genap ya?
Soal mengenai pola bilangan matematika maupun jumlah deret seperti itu seringkali muncul dalam soal olimpiade. Untuk memudahkan pengerjaan soal seperti itu perlu dilakukan manipulasi bentuk 🙂
wow itu angka semua mas? 😀
Enggak semua mas Andank, ada hurufnya juga kok 😀
Terimakasih 😀
Kebetulan baru dibahas di les
Jadi bisa buat nambah2 deh
hehehehhehe
Iya sama-sama, sering-sering aja mampir ke sini 🙂
Wah matematika adalah pelajaran yang paling tidak saya kuasai, nilai matematikaku jeblok semua… hehehe
Harus sering2 maen kesini ah, biar tambah pinter matematika 😀
Monggo mas, silakan sering-sering saja mampir ke sini. Sangat disarankan malahan 🙂
Tolong bantu ya mas
Jika V menyatakan volume dan s luas permukaan dari sebuah balok berukuran a x b x c maka 1/v =…
a. s/2 (a+b+c)
b. 2s/a+b+c
c. 2/s (1/a + 1/b + 1/c)
d. 2s (a+b+c)
tolong bantu secepatnya ya..
soal yg lebih jelas ada di buku MM kelas VIII jilid 2 penerbit erlangga hal 323 no. 18
makasiii
Maaf baru sempat bales….
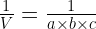
 maka
maka
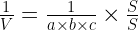




Kalikan kedua ruas dengan 1, karena
Jadi, jawabannya adalah pilihan C
Apakah sudah jelas? atau ada yang masih ditanyakan?
makasi ya mas…
😀
Iya sama-sama 🙂
kak…
tny dunk…
hhehehe….
ini ad soal…
Misalkan f(x)=2/(4^x+2) untuk x∈R hitunglah f(1/21)+f(2/21)+f(3/21)+⋯+f(20/21)
tolong yy…
jwbn.a sianx ini bsa g…
hhehehe….
Ya nanti Insya Allah kalo sempat saya publish pembahasan jawabannya, itu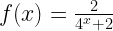 atau
atau 
ya yang depan,,,,,
tny donx kak….
hihi….
Sederhanakan bentuk berikut ini
a^3/((a-b)(a-c))+b^3/((b-a)(b-c))+c^3/((c-a)(c-b))
Iya, insya Allah nanti saya tuliskan pembahasannya.
kakak yang baik.! mau nanya nich
carilah semua fungsi ƒ:R→R sedemikian hingga
{ƒ(x) – ƒ(y)}/{(x-y} = {ƒ(x).ƒ(y)}/{xy} dan x tidak samadengan y
maaf banget urgent banget kakak
Itu syaratnya apakah hanya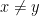 saja?
saja? maka penyebutnya = 0.
maka penyebutnya = 0.
Karena kalau
ka Tolong Kasih Soal Donk Garis Singgung Lingkaran Tapi 6 aja………Plizzzzzzz…..Mohon bantuannya
Untuk materi garis singgung persekutuan linkgaran saya pernah menuliskannya. Di sana juga terdapat beberapa soal yang ditanyakan oleh pengunjung, beserta penyelesaiannya. Silakan dicek di bagian komentar.
http://dumatika.com/garis-singgung-persekutuan-2-lingkaran
Mudah-mudahan sudah ada 6.
Ada yang bisa share soal2 OSN utk SMU ?
tolongin dung
akar(6+akar6……(sampek tak hingga))=x
berapa nilai x
makasih/….
Kedua ruas dikuadratkan, sehingga diperoleh
Secara lengkap ditulis sebagai berikut:
Dari persamaan terakhir, di dapat
Jadi jawabannya adalah
Semoga bisa membantu 🙂
kk mtak tlong cieh 4 Log(A+2) – 4 Log(apngkat2-4)=?
brpa ye kk
Bentuk soalnya seperti ini ya?

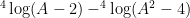
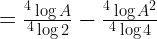
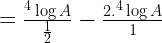


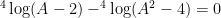
Baiklah, sebenarnya lebih baik ditanyakan di postingan Soal-soal logaritma tapi ya sudah tidak apa-apa 🙂
Pertama, gunakan sifat-sifat dasar pada logartima
Jadi,
Sudah jelas atau masih ada yang ditanyakan?
4 log(a+2)-4 log(apangkat2-4)= ?
kak mw tanya 3 soal,, soalnya ni gmna pnyelesaiannya,, mohon bantuannya yah kak:)please
1. (1/1-p)pangkat4 (1/1+p)pangkat-6 (1+p/1-p)pangkat-5 ?
2. (xpangkat2/3ypangkat-4/3: ypangkat2/3xpangkat2)pangkat-3/4 ?
3. jika diketahui a=4+akar3 dan b=4-akar3, maka nilai a pangkat2 + b pangkat2-2ab?
Pembahasannya sudah saya berikan di postingan tersendiri, silakan kunjungi Soal dan pembahasan dari Diach
cara mengisi oprasi bilagan bulat