Materi Matematika

Jenis Segitiga dan Garis Istimewa pada Segitiga

Sholihin 21 Februari 2012 27 Comments

Seperti yang sudah kalian ketahui, segitiga merupakan bangun datar yang dibatasi oleh tiga buah garis lurus yang saling berpotongan dan membentuk tiga buah sudut. Titik potong garis tersebut merupakan titik sudut segitiga. Segitiga sendiri ada beberapa macam, misal segitiga sama kaki, segitga siku-siku, dan sebagainya yang dibagi berdasarkan panjang sisi dan juga besar sudut pembentuknya.

Jenis-jenis segitiga berdasarkan panjang sisinya

Berdasarkan panjang sisinya, segitiga dibagi menjadi:

  1. Segitiga sama sisi, yaitu segitiga yang ketiga sisinya sama panjang. Akibatnya, ketiga sudutnya pun sama besar, yaitu 60°.
  2. Segitiga sama kaki, yaitu segitiga yang mempunyai dua sisi sama panjang. Segitiga ini mempunyai dua sudut yang sama besar, yaitu sudut yang berada di sisi yang sama panjang, atau sering disebut kaki segitga.
  3. Segitiga sembarang, yaitu segitiga yang ketiga sisinya berbeda panjangnya. Akibatnya, ketiga sudut segitiga tersebut juga tidak ada yang sama.

Jenis Segitiga berdasar panjang sisi

Jenis-jenis segitiga berdasarkan besar sudutnya

Berdasarkan jenis sudut pembentuk segitiga, maka segitiga dapat dibagi menjadi:

  1. Segitiga siku-siku, yatiu segitiga yang besar salah satu sudutnya 90° atau siku-siku. Hipotenusa atau sisi miring adalah sisi di hadapan sudut siku-siku tersebut.
  2. Segitiga tumpul, yaitu segitiga yang besar salah satu sudutnya lebih dari 90° atau sudut tumpul.
  3. Segitiga lancip, yaitu segitiga yang ketiga sudutnya kurang dari 90° atau sudut lancip.

jenis segitga berdasarkan besar sudutnya

Dengan memperhatikan panjang sisi-sisi segitiga, kita dapat menentukan apakah suatu segitiga termasuk segitiga siku-siku, tumpul, maupun segitiga lancip. Caranya adalah segitiga berikut, misal diketahui segitiga dengan panjang sisi a, b, dan c dengan c adalah sisi terpanjang.

Jenis segitiga

  • Jika c² = a² + b² maka segitiga tersebut merupakan segitiga siku-siku.
  • jika c² > a² + b² maka segitiga tersebut merupakan segitiga tumpul.
  • jika c² < a² + b² maka segitiga tersebut merupakan segitiga lancip.

Garis istimewa dalam segitiga

Dalam segitiga, terdapat beberapa garis-garis istimewa, di antaranya sebagai berikut:

Garis berat, yaitu garis yang ditarik dari titik sudut ke pertengahan sisi di hadapannya. Ketiga garis berat melalui satu titik yang disebut titik berat. Titik berat membagi masing-masing garis berat dengan perbandingan 2 : 1.

Garis berat segitiga
Garis Berat Segitiga

Pada gambar di atas, garis berat ditandai dengan garis warna biru, yaitu AD, CF, dan BE. Garis berat tersebut berpotongan di titik P, yang merupakan titik berat. Titik berat merupakan titik pusat masa, bermanfaat dalam hal keseimbangan. Perbandingan garis berat adalah AP : PD = BP : PE = CP : PF = 2 : 1

Garis bagi, yaitu garis yang ditarik dari sebuah titik sudut dan membagi sudut tersebut menjadi dua bagian sama besar. Ketiga garis bagi melalui satu titik yang disebut titik bagi. Titik bagi merupakan pusat lingkaran dalam segitiga.

Garis bagi segitga
Garis Bagi Segitiga

Pada gambar di atas, AD, EC dan BG adalah garis bagi, sedangkan titik F merupakan titik bagi, atau titik pusat lingkaran. Jika dari titik F ditarik garis tegak lurus ke sisi segitiga, maka akan terbentuk jari-jari lingkaran dalam segitiga, misal garis FN. Jika dari titik F dibuat lingkaran dengan jari-jari FN terlukislah lingkaran dalam segitiga.

Garis tinggi, yaitu garis yang ditarik dari titik sudut dan tegak lurus sisi di hadapannya. Ketiga garis tinggi melalui satu titik yang disebut titik tinggi. AH, BI, dan CJ merupakan garis tinggi.

garis tinggi segitiga
Garis Tinggi Segitiga

Garis sumbu, merupakan garis yang tegak lurus pada pertengahan garis/sisi itu. Perhatikan gambar berikut, garis sumbu ditandai dengan garis yang berwarna biru. Ketiga garis sumbu berpotongan di satu titik, yaitu titik O dan merupakan titik pusat lingkaran luar segitiga.

garis sumbu
Garis Sumbu Segitiga

Kiranya sekian sedikit ringkasan mengenai jenis-jenis segitiga beserta garis-garis istimewa dalam segitiga, moga bisa bermanfaat. Teorema yang berhubungan dengan segitiga juga sangat banyak, misal ada dalil stewart, kesebangunan, teorema garis bagi, dan masih banyak yang lainnya. Silakan dieksplorasi.

27 Replies to “Jenis Segitiga dan Garis Istimewa pada Segitiga”

  4. Dulu Saya pernah baca tentang eksperimen garis berat. Pertama buat segitiga/elemen sembarang dari kertas, lalu tarik semua sudut ke tengah. (Atau ada juga yang praktek pake jarum & gravitasi)
    Nah, titik temunya itu untuk kesetimbangan. Angkat pensil ke atas, letakkan titik temu tepat di ujung pensil, pasti sembang.

    Balas

    1. Iya mas Taufik, benar seperti itu. Dulu pas SD/SMP juga pernah mainan seperti itu, ada juga yang pake buku tulis/kertas lain. Prinsipnya adalah mencari titik berat/pusat masa suatu benda 🙂

      Balas

  5. aku terbantu sekali dengan adanya Dumatika.com ini..
    klo bisa, ada link download nya dong!!
    makasih

    Balas

    1. Senang bisa membantu, mudah-mudahan bisa bermanfaat.
      Link download apa ya yang dimaksud? di menu navigasi bagian atas ada panel unduh, silakan kalau mau download menuju ke navigasi tersebut.

      Balas

        1. Kalo materi belum ada fasilitas downloadnya, baik itu dalam versi pdf maupun cetak. Mungkin suatu saat nanti bisa dipertimbangkan.
          Untuk save artikel bisa menggunakan save as.

          Balas

  7. mas, riska minta bantu lagi…
    ada soal:
    pada segitiga ABC, dengan a:28, b: 30, c: 26, tentukan jarak antara pertengahan AC dengan sisi BC?
    makasih mas…

    Balas

    1. Misal pertengahan AC adalah titik D, dan titik E terletak di sisi BC sedemikian hingga $latex DE \perp BC. Maka DE adalah jarak pertengahan AC dengan sisi BC (ingat, jarak adalah garis terpendek, dan tegak lurus).
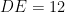
      Tarik garis dari titik A ke garis BC, misal garis AF sehingga AF \perp BC, maka AF merupakan garis tinggi segitiga ABC.
      S = \frac{1}{2}(30+28+26)=42
      Luas ABC = Luas ABC
      \frac{BC \times AF}{2} = \sqrt{42(42-30)(42-28)(42-26)}
      \frac{28 \times AF}{2} = \sqrt{112896}
      14AF = 336
      AF = 24
      Segitiga AFC sebangun dengan segitiga CDE, gunakan perbandingan.
      \frac{CD}{AC} = \frac{DE}{AF}
      \frac{15}{30}=\frac{DE}{24}
      DE = 12
      Jadi jarak pertengahan AC dengan sisi BC adalah 12 cm.
      Apakah jelas? Mungkin masih ada kesalahan, mohon koreksinya.

      Balas

    2. mas, kalau soal begini, gmna penyelesaiannya ya,
      suatu trapesium dengan sisi-sisi sejajar 10 cm dan 73 cm kaki-kakinya 25 cm dan 52 cm. tentukan tinggi dan luas trapesium?

      Balas

      1. Misal tinggi = t, maka tinggi pada sisi miring (kaki) yang 25 cm sama dengan tinggi pada sisi miring yang 52 cm.
        Pada sisi 25, ada segitiga siku-siku dengan sisi miring = 25, tinggi = t, dan alas = x. Gunakan phytagoras,
        t^2 = 25^2 - x^2 = 625 - x^2.
        Pada segitiga siku-siku dengan sisi miring 52 cm, tinggi = t dan alas = 63 – x.
        t^2 = 52^2 - (63-x)^2 = -1265 + 126x - x^2.
        t^2 = t^2
        625 - x^2 = -1265 + 126x - x^2
        625+1265 = 126x
        x = \frac{1890}{126}
        x = 15
        t = \sqrt{25^2 - 15^2} = \sqrt{625 - 225} = \sqrt{400} = 20
        Jadi tinggi trapesium 20 cm
        \text{Luas trapesium} = \frac{(73 + 10) \times 20}{2} = 830
        Jadi, luas trapesium 830 cm²
        Apakah sudah jelas?

        Balas

  8. misi min, bisa bantu ane g? ane dpt soaL kya gini :
    1). Sisi tegak & sisi atas suatu trapesium sama kaki dengan A. Tentukan besar sudut alas trapesium itu supaya luasnya sebesar mungkin!
    (dik: phi / 3 , 3A-kuadrat akar 3 / 6)

    2). Sebuah peti yg terbuka diatas (tanpa tutup) alasnya merupakan bujur sangkar & isinya diketahui V. Tentukan ukuran peti tsb supaya bahan yg diperlukan untuk membuat peti itu sehemat mungkin!
    (dik: tinggi peti= 1 / 2 sisi aLas)

    toLong d bantu min, ane g ngerti sama tuh soaL…
    mksh 😀

    Balas

    1. Ini soal kelas berapa kalo boleh tahu?
      Untuk nomer 1 kurang begitu paham soalnya, ada yang aneh. Apakah yang dimaksud sisi tegak sama dengan kaki trapesium? Trus phi/3 dan 3A-kuadrat akar 3 / 6 itu disebelah mana? Kalo ada sertakan gambarnya.

      2. Misal bujur sangkar berukuran s, maka tinggi peti = t. = \frac{1}{2}y
      V = s \times s \times t = s^{2}t
      V = s^{2}t \Leftrightarrow t = \frac{V}{s^2}
      Luas = s^2 + 4(s \times t)
      Luas = s^2 + 4s(\frac{V}{s^2}
      Luas = s^2 + \frac{4V}{s}
      Agar luas minimum, maka L' = 0
      2s - \frac{4V}{s^2} = 0
      2s = \frac{4V}{s^2}
      s^3 = 2V
      s = \sqrt[3]{2V}
      Jadi agar luasnya minimum maka ukuran peti adalah \sqrt[3]{2V} \times \sqrt[3]{2V} \times \frac{1}{2}\sqrt[3]{2V}
      Kalau soalnya lebih jelas dan lengkap lagi penjelasannya akan saya tulis di postingan khusus.

      Balas

  10. bantu aku y. da soal ni… plz….
    segitiga ABC siku2 d B,dengan CD adalah garis bagi sudut c.DE tegak lurus AC. AB = 10cm.berapakah panjang BD?

    Balas

    1. Yang diketahui hanya panjang AB = 10 cm? yang lain tidak ada yang diketahui lagi?
      Baiklah, akan coba saya buatkan pembahasannya dan saya posting segera, secepat yang saya bisa.

      Balas

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *