Dalam matematika, menggambar sebuah sudut menggunakan penggaris lurus maupun penggaris busur adalah hal yang sudah biasa. Bahkan sejak dari SD kita sudah diajarkan cara menggambarkan sudut, dan kita harus bisa menguasainya sampai jenjang SMP, SMA maupun seterusnya. Seperti yang telah kita ketahui, sebuah sudut bisa dinotasikan dengan tanda “
Kita dapat membagi besar sebuah sudut dengan menggunakan alat berupa penggaris dan juga jangka. Berikut ini merupakan cara mudah untuk membagi sebuah sudut menjadi dua sama besar. Jangan lupa siapkan alat-alatnya ya, yaitu penggaris dan juga kompas.
Berikut Langkah-langkah Membagi Sudut Menjadi 2:
Langkah pertama, coba perhatikanlah gambar berikut. Di bawah ini terdapat sebuah sudut, yaitu sudut ABC dengan besar sudut 
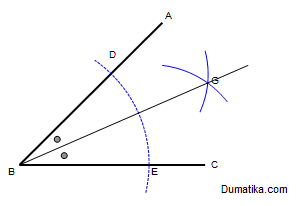
Dengan titik pusat B, lukislah busur yang melintasi AB dan AC. Caranya, gunakan jangka yang berpusat di titik B untuk membuat busur sehingga memotong garis AB dan AC. Titik potong tersebut kita beri nama di titik D dan E. Untuk lebih jelasnya, perhatikan gambar langkah (1) di bawah ini.
Langkah kedua, dari titik D dan titik E buatlah busur lingkaran dengan lebar jangka/jari-jari yang harus sama. Caranya, misal pertama dengan titik pusat E, jangkakan busur lingkaran.
Kemudian, tanpa merubah ukuran jangka ulangi cara yang sama dengan titik pusat D. Dari kedua busur lingkaran tersebut akan saling berpotongan. Misalkan titik potongnya adalah titik G.
Pada gambar di atas, terlihat bahwa titik G adalah merupakan titik perpotongan antara busur yang berpusat di titik D dan juga busur yang berpusat di titik E. Langkah ketiga adalah menghubungkan titik G dengan titik B. Garis BG merupakan garis bagi yang membagi sudut ABE menjadi dua sama besar.
Garis BG sebagai garis bagi telah membagi sudut ABC menjadi dua sama besar, yaitu
Jika kita hubungkan titik G dengan titik D, dan titik G dengan titik E makan akan terbentuk bangun layang-layang. Pada sifat layang-layang, diagonal yang panjang juga membagi sudut menjadi dua sama besar. Ada beberapa kesalahan yang sering dilakukan oleh siswa ketika membagi sudut dengan cara seperti yang telah dijelaskan di atas. Kesalahan yang sering dilakukan adalah ketika pada langkah 2b. Ketika melukis busur pada langkah 2b, jarak busur dengan titik pusat, atau disebut jari-jari, haruslah sama dengan pada langkah 2a. Tetapi siswa ada yang berbeda jari-jarinya, sehingga sudut yang terbagi menjadi tidak sama.
Yang perlu diperhatikan, jari-jari pada langkah 1 dengan jari-jari pada langkah 2a maupun 2b boleh sama boleh juga tidak. Yang terpenting adalah jari-jari busur lingkaran pada langkah 2a dan langkah 2b harus sama. Bagaimana, mudah bukan cara membagi sudut menjadi dua sama besar? Jika sudah menguasai cara ini, maka untuk melukiskan sudut-sudut istimewa seperti sudut 90°, 45°, 60°, maupun sudut 30° tidak akan menemui kesulitan. Kalau ada pertanyaan atau ada yang masih kurang jelas, silakan ditanyakan melalui komentar di bawah.
Artikel ini bermanfaat? Jangan lupa klik tombol share di bawah ini untuk berbagi kepada teman-teman yang lain.
WAH wah.. subuh2 udah baca postingan matematika nih.. tambah melek.
selamat berpuasa gan.
salam kenal
Selam kenal juga mas Aji, selamat menjalankan ibadah puasa Ramadhan 🙂
cara ini memang mudah bagi kita, tapi kadang anak2 kita seperti waktu dulu kita pertama belajar harus diberi pengertian berulang kali agar mudah dipahami. nice share
Trimakasih, matematika tanpa latihan tidak akan berhasil. Siswa harus praktik mengerjakan sendiri agar bisa, tidak hanya melihat contoh saja.
Karna kalau tidak dicoba dan hanya dibaca siswa belum tentu bisa.
Angkat tangan, “Gak paham Pak Guru”,
Hahaha kaya lagi ditodong aja angkat tangan. Aku juga gak begitu paham kok matematika 😀
Ingat saat SMP…
Juga saat bikin sudut istimewa tanpa busur derajat
Insya Allah nanti menyusul cara melukis sudut istimewa tanpa menggunakan busur derajat pak Mars, doakan saja biar cepet publish 🙂
Pernah inget ini mas saya belajar seperti di atas. Tapi lupa pas kelas berapa. Kalo sekarang udah lupa mas, karena gak pernah bersentuhan lagi dengan perhitungan semacam itu hehehe
Anyway, akhirnya mas nulis lagi di blog ini 🙂
Iya mas, kalau kurikulum dulu mungkin Mas Faisal mengalami pas SMP kelas 1 ya kalo gak sala?
Hehehe jadi malu, sebenarnya ada beberapa post di draft, tapi ya itu belum sempat meneruskan lagi. Makasih mas semangatnya 🙂
sip.. mengingatkanku pada matematika SMP..
salam.
Saya suka sekali kalo pelajaran matematika dasar macam ini.. Hihi
Selamat datang di dunia matematika, Mae 🙂
Sampe sekarang masih suka matmatika kan? Percayalah, sampe kapanpun matematika akan tetap selalu dipakai 🙂
kalau gak salah, ini pelajaran SMA kelas 1 ya?
kalau gak salah pelajaran menggambar sudut
Untuk kurikulum sekarang di SMP pun sudah ada mas Fariz 🙂
terimakasih atas postingannya,, insyaAllah sangat bermanfaat, krn guru mesti update terus ni,..
Sama-sama, senang bisa membantu. Mudah-mudahan bisa bermanfaat 🙂
Mas Sholihin Pinter Matematika ya,Kalo saya malah paling gak bisa hahaa..
Ini masih belajar kok mas Rudi, lagian saya juga gak pinter matematika 🙂
Deskripsinya sangat mudah dicerna, Insya Allah bermanfaat sekali.
Salam!
Terimakasih, masih belajar mudah-mudahan bisa bermanfaat untuk orang lain 🙂
Yang menarik untuk ditanyakan juga ke siswa adalah setelah mereka mengetahui cara membagi sudut dengan teknik ini, apakah mereka yakin bila dua sudut yang dihasilkan sama besar lalu apa alasannya.
Saya rasa pertanyaan semacam ini penting agar siswa selalu berpikir kritis dan tentunya tidak mudah lekas percaya dengan apa yang didapat. Akan tetapi selalu mencoba mencari alasan logis di balik semua keterangan yang diperoleh
Betul sekali mas Tutur, setuju. Siswa harus diberikan pertanyaan-pertanyaan yang membangun seperti itu agar siswa menemukan sendiri jawabannya dan benar-benar percaya dengan jawabannya tersebut. Sebagai seorang guru jangan sering-sering memberikan pernyataan bahwa a adalah a, biarlah siswa menemukan sendiri dan percaya kalau a adalah a. Guru hanya sebagai fasilitator saja 🙂
sipp…dapet ilmu, lumayan utk mengingatkan kembali
thanks
mudah-mudahan dengan membuat gampang matematika, banak murid ke depannya yg pada suka mas…
Aamiin pak, matematika sekolah tidak sesulit seperti yang dibayangkan dan ditakutkan oleh para siswa. Kalau sudah mengenal matematika, maka dengan sendirinya akan memahami matematika sekolah dengan mudah dan cepat 🙂
jadi teringat saat smp nich
@tutur:
Untuk meyakinkan bahwa sudut tersebut terbagi dua sama besar, kita bisa menjelaskan dengan sifat lingkaran atau bangun geometri lain seperti layang-layang yang mas Sholihin jelaskan pada post.
Dari langkah-langkah tersebut, diperoleh layang-layang BEGD. Dari sifat layang-layang sendiri jelas bahwa BG membagi sudut B menjadi dua sudut sama besar.
CMIIW 😀
Betul mas, untuk tingkat sekolah menengah sepertinya dengan sifat layang-layang sudah cukup dapat dicerna oleh para siswa 🙂
aku dah lupa yang beginian broooo 😛
Lebih basic lagi dengan kekongruenan pada segitiga
makasih infonya ya…:)
makasih infonya ya…:)
bagai mana cara membagi sudut mmenjadi 3bagian menjadi sama besar
Untuk membagi sudut menjadi 3 sama besar bisa menggunakan alat namanya Penggaris Kapak Tomahawk, jadi kita harus mempunyai penggaris yang berbentuk seperti kapak tomahawk tersebut.
Ataum, bisa menggunakan cara seperti berikut yang diambil dari http://id.answers.yahoo.com/question/index?qid=20090616004826AAp0Ota
Dengan bantuan jangka.
Misalkan ada gambar sudut CAB = 90, titik A sebagai titik sudut.
1.Buat lingkaran dengan titik A sebagai pusat, sehingga mendapatkan titik perpotongan dengan AB = D.
2.Buat lingkaran dengan r yg sama dari titik D sebagai pusat, sehingga mendapatkan titik perpotongan dengan Lingkaran pertama = E.
3.Maka ADE adalah segitiga sama kaki = sama sudut = 60.
4.Dengan bantuan jangka, bagi dua sudut DAE :
Dari titik D dan dari titik E, titik persilangan jangka ini (F) kalau ditarik ke titik A, merupakan pembagi sudut DAE sama besar = 30.
5.Hasilnya Sudut CAB sudah terbagi 3 sama besar :
CAE = 30
EAF = 30
FAB = 30
Demikian semoga sesuai dengan apa yg dimaksud.
info yang sangat menarik gan ichink
Nah, kalo ini aku udah pernah belajar di SMP, gampang betul 😀
Bagaimana cara membagi tiga suatu sudut?
Di komentar sebelumnya pernah ada yang menanyakan hal yang sama, silakan dibaca-baca dahulu komentar sebelumnya 🙂
Contoh yg diberikan cara membagi tiga sudut 90 derajat saja. Bgmna kalau membagi tiga sudut lainnya dgn jangka? Terimakasih.