Dalam kehidupan sehari-hari, sering kita menjumpai hal-hal yang berhubungan dengan barisan maupun pola bilangan. Misalnya nomor rumah mengikuti pola bilangan ganjil dan pola bilangan genap. Pada kesempatan kali ini, coba sedikit membahas pola bilangan, khususnya barisan dan deret Aritmatika.
Apa yang dimaksud barisan dan deret Aritmatika?
Barisan Aritmatika
Suatu barisan bilangan disebut barisan aritmatika jika selisih dua suku yang berurutan selalu tetap. Selisih dua suku yang berurutan disebut dengan beda, atau dinotasikan dengan
. Sedangkan suku pertama
. Bentuk umum barisan aritmatika adalah sebagai berikut:
dengan:
Contoh barisan aritmatika dengan
Jika merupakan barisan aritmatika, maka berlaku
Jika pada barisan artimatika disisipkan k buah bilangan sehingga terbentuk barisan aritmatika baru, maka dengan k adalah banyaknya bilangan yang disisipkan.
Suku ke-n Barisan Aritmatika
Untuk mencari suku ke-n barisan aritmatika perhatikan langkah berikut:
Jadi, rumus suku ke-n barisan aritmatika
Deret Artimatika
Jika merupakan barisan aritmatika, maka
merupakan deret aritmatika.
Jumlah n suku Deret Aritmatika
Jumlah n suku pertama deret aritmatika dinotasikan dengan .
Untuk mendapatkan rumus jumlah n suku pertama deret aritmatika perhatikan langkah-langkah berikut:
atau karena
maka
Keterangan:
Suku ke-n dari barisan aritmatika juga bisa dicari menggunakan rumus berikut:
Rumus Suku Tengah Barisan Aritmatika
Suatu barisan aritmatika dengan banyaknya suku dimana
maka untuk mencari suku tengahnya dapat digunakan rumus:
Keterangan:
Ini hanya sedikit uraian mengenai barisan dan deret Aritmatika. Masih banyak pola bilangan yang lain. Ada pertanyaan? Silakan bertanya melalui kolom komentar di bawah.

hadeuuuh ane nyerah deh klo dikasih rumus beginian mah hahah.,
Kata Ryan de’Nasib jangan menyerah om hahaha 😀
gak papa om, itung-itung belajar lagi. Mesti dulu dah pernah kan dapet kaya ginian? hee….
emank sih dulu aku paling pinter disekolah ma yg ginian hahah., sampe2 gurunya sayang banget ma aku., beuh., apalagi gurunya masih gadis., cantik lagi ahahah., ko ga nyambung ya,. 😀
mas, kalo Sn yang ditanya dan selisih yang diketahui gimana cara?
Soal lengkapnya bagaimana?![S_n = \frac{n}{2}[2a + (n-1)\times selisih] S_n = \frac{n}{2}[2a + (n-1)\times selisih]](https://s0.wp.com/latex.php?latex=S_n+%3D+%5Cfrac%7Bn%7D%7B2%7D%5B2a+%2B+%28n-1%29%5Ctimes+selisih%5D+&bg=ffffff&fg=000000&s=2)
Biasanya untuk mencari Sn maka suku pertama/suku yang lain, dan selisih juga harus diketahui. Kalau yang diketahui hanya selisih rumus Sn nya sepertinya tidak bisa dicari, hanya mentok di
eh sori, n nya juga diketahui mas. udah tak coba rumusnya. ketemu mas. hahaha males buka buku eh ketemu disini langsung tak coba pake ms.excel eh dapet. mantep dah
Yupsss, memang harusnya ada faktor yang diketahui lagi.
Met belajar ya….. 😀
Kalo gak salah kemaren pas semester awal sempet belajar juga nih deret aritmatika gini, tapi udah lupa sekarang mah,hehehe
Ayo mas Faisal, diinget-inget lagi 😀
Mantap deret-deret aritmatikanya mas…
Iya mas, makasih. Sebenarnya masih kurang lengkap, tapi repot juga kalo harus nulis semuanya pak.
komplit banget mas,,
terima kasih:D
Iya sama-sama, met belajar ya.
paling suka sama barisan sama deret aritmatika pas sma.
pas UN sama SNMPTN, pasti nyari soal ginian dulu 😀
Iya mas, bener tuh pola bilangan juga bakalan muncul di psikotes sekalipun 🙂
aduch…
aku paling benci.,.. ama nyari soal kayak gini…
Benci kenapa? 🙂
Bisa dipelajari kok, tenang aja.
hhuuuffff,,,, pokoknya ,, aku benci kalo pakek gitu gituan,,, bikin pusing kepala aja…:-(
Selain sekedar buat ikut psikotes sih ini banyak kepake di bidang computer science (kebetulan gw orang komputer sih). Kemarin juga keluar di soal tes buat pegawai baru pas ngelamar kerja di bagian soal matematika & logika. Berhubung ini bisa aja keluar di tes pas kita ngelamar kerja, penting dong buat dipelajarin. 😀
Sebenernya nggak ribet-ribet amet juga sih, cuma emang agak gampang-gampang susah pas nebak-nebak polanya.
Yupps mas, matematika banyak dipake di segala bidang 😀
nnya lg yy kak…
ad soal bgni
Suatu barisan bilangan : 4-6-1-6-8-2-2-8-10-3-3-….-…… Bilangan selanjutnya adalah….
ini soal.a tu termasuk deret aph yy…???
trus cra pngerjaanya gmna….
aq nyri” g ktmu”i…
🙁
Kalo menurutku jawabannya 3 dan 10
Penjelasannya gini:
lihat dulu angka 1, 2 dan 3. Sebenarnya itu adalah perulanga 1 sebanyak 1 buah, angka 2 sebanyak 2 buah [2 – 2] dan sebelum perulangan itu selisih bilangannya adalah 2 [ 4 – 6, 6 – 8, 8 – 10]
Jadi kalo diterusin seperti ini
4 – 6 – 1 – 6 – 8 – 2 – 2 – 8 – 1 0 – 3 – 3 – 3 – 10 – 12 – 4 – 4 – 4 – 4 – 12 – 14 – 5 – 5 – 5 – 5 – 5 – 14 – 16 – ……
oooooo…..bgtu yy…???
embb….
mkasiiiiii………..
🙂
Iya, kurang lebih seperti itu. Sama-sama.
wew…mantap, untuk jawaban yg diatas
Trimakasih, tapi jawaban yang mana yah? yang pola bilangan dari u-tarii po? 😆
kk, kalau pada deret aritmatika., rumus banyak suku pada deret aritmatika nya apa??
Contoh:
4 12 20 … 132
ditanya banyak suku pada deret diatas berapa?
rumusnya gmana??
Itu adalah mencari nilai n, . Suku terakhir menunjukkan banyaknya n.
. Suku terakhir menunjukkan banyaknya n.




pada deret tersebut diketahui a = 4, b = 8
Rumus suku ke-n adalah
Karena suku terakhir adalah suku ke-17, maka banyaknya suku ada 17.
Moga bisa dipahami.
penjelasann yang ckupp memuasknn !
syngx g bsah di COPAZ !
tp… ttp sj aq ajuninn jempoll !
mantapp !
penjelasan yang cukupp memuaskann,,
syangx g bsah d i COPAZ !
tp,,,tetapp ajha aq ajunin jempolll !
Mantapp !
Sipp, makasih.
Sebenarnya bisa dikopas kok, asal tau tricknya. Blognya sengaja diprotect karena udah beberapa kali artikel dikopas mentah-mentah tanpa memberikan link sumbernya.
plis donk kasitau cara biar bisa di copaz, perlu bgt nih artikel
Gunakan browser chrome, opera, atau internet explorer. Maka artikel bisa dicopy, silakan gunakan kesempatan tersebut dengan bijaksana.
Maksudnya di copas ke mana. Kalau ditulis link sumbernya boleh di copas?
Boleh kok, tapi kalau bisa jangan kopas sama persis, untuk menghindari duplikat kontent. Karena nanti blogmu akan dianggap kopi paste.
Asw. prtanyaan sy, Deret Aritmetika dikthui U3+U6+U9+U12 = 72 ditanya jumlah 14 suku pertma ??
Mohon penjelasan, Trmkasih
Walaikumsalam.







DItanya jumlah 14 suku pertama, dari rumus Sn maka S14 bisa dicari.
Apakah sudah jelas?
Ya,, sudah jelas sekali,, harus paham soal dan mengaitkan dg rumus yang ada,, itu yg sy gk bisa. tpi trimakasih ats pnjlsnnya
Itulah mengapa konsep dasar kadang jauh lebih penting daripada cara praktis, karena seringkali kita dihadapkan pada soal yang membutuhkan kreasi dan pengembangan konsep.
Sama-sama, moga bisa bermanfaat.
mas,mw tanya, kalau suku ke 7 suatu barisan adalah 27 dan suku ke 12 adalah 37, berapakah suku ke 14,
makasi
Ini barisannya diketahui aritmatika atau tidak? atau hanya sebuah barisan bilangan?
Misal aritmatika,
U7 = a + 6b = 27 ………..(1)
U12 = a + 11b = 37 ………….(2)
Lakukan substitusi/eliminasi pada persamaan (1) dan (2)
a + 11b = 37
a + 6b = 27
________________-
5b = 10
b = 2 ==> a = 15
Suku ke-14
U14 = a + 13b = 15 + 13(2) = 41
Jadi suku ke-14 nya adalah 41
suatu barisan bilangan 2,6,12,20,……..suku yang ke 20 adalah….
U1 = 2 = 1 x 2
U2 = 6 = 2 x 3
U3 = 12 = 3 x 4
U4 = 20 = 4 x 5
Un = n x (n + 1)
U20 = 20 x (20 + 1) = 20 x 21 = 420
Barisan di atas merupakan pola bilangan persegi panjang, silakan dibaca untuk lebih jelasnya.
jika hari ini adalah hari jumat, maka 1000 hari lagi hari apa?
rumus penyelesaiannya seperti apa?
tmksh
1 Minggu ada 7 hari
1000 hari dibagi 7 hari adalah 142, sisanya 6 hari.
6 Hari setelah hari Jum’at adalah hari kamis.
Berari jika hari ini jum’at, 1000 tahun lagi adalah hari kamis.
ini gimana mas… suku tengah deret aritmatika 18,suku terakhir 33,suku ke lima 23,, berapa banyak deret
Berdasarkan rumus suku tengah seperti di atas,
![U_k = \frac{1}{2}[U_1 + U_{2k-1}] U_k = \frac{1}{2}[U_1 + U_{2k-1}]](https://s0.wp.com/latex.php?latex=U_k+%3D+%5Cfrac%7B1%7D%7B2%7D%5BU_1+%2B+U_%7B2k-1%7D%5D&bg=ffffff&fg=000000&s=0)
![18 = \frac{1}{2}[a + 33] 18 = \frac{1}{2}[a + 33]](https://s0.wp.com/latex.php?latex=18+%3D+%5Cfrac%7B1%7D%7B2%7D%5Ba+%2B+33%5D&bg=ffffff&fg=000000&s=0)

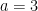



![U_n = [a + (n - 1)b] U_n = [a + (n - 1)b]](https://s0.wp.com/latex.php?latex=U_n+%3D+%5Ba+%2B+%28n+-+1%29b%5D&bg=ffffff&fg=000000&s=0)
![33 = [3 + (n - 1)5] 33 = [3 + (n - 1)5]](https://s0.wp.com/latex.php?latex=33+%3D+%5B3+%2B+%28n+-+1%295%5D&bg=ffffff&fg=000000&s=0)



Suku ke-5
Suku terakhir menyatakan banyaknya suku
Jadi, banyaknya suku ada 7 buah.
Apakah sudah jelas? Semoga bisa membantu.
pingin tanya tw gag soal ini Berapa banyak bilangan antara 1-500 yang tidak habis dibagi 3&5?
Bilangan yang habis dibagi 3 dan 5 berarti habis dibagi 15.
Bilangan tersebut adalah 15, 30, 45, …, 480 yang membentuk barisan aritmatika.
a = 15, b = 15 maka didapat n = 32
Banyaknya barisan tersebut bisa dicari menggunakan rumus pada barisan aritmatika, yaitu ada 32.
Bilangan yang tidak habis dibagi 3 dan 5 berarti bilangan selain di atas, banyaknya ada 500 – 32 = 468
CMIIW
A.] cari bilangan yang habis dibagi KPK dari 3 dan 5 yaitu 15 :
15 + (n – 1) 15 = 500
15n = 500
n = 33 sisa 5
ada 33 bilangan
E.] bilangan yang tidak habis dibagi 3 dan 5 :
= (500 – 2) – 33
karena antara 1-500
= 498 – 33
= 465 bilangan
(via yahoo answer) CMIIW
thank’s gan, sekalian sumbang ki$$
wah….rumus jumlah deretnya bsa dipake nih buat ngerjain tabel akutansi…..hehe
Banyak ilmu matematika yang diterapkan juga di ilmu yang lain, karena matematika sebagai ilmu universal jadi saling terkait juga dengan ilmu yang lain.
Mudah-mudahan yang saya sampaiakan bisa bermanfaat 🙂
bantuin donggg….
jika jumlah 10 suku pertama suatu deret aritmatika adalah 110 dan jumlah 2 suku berturut-turut berikutnya adalah -2, maka jumlah 2 suku pertama deret itu adalah…
dibantu yaaa.. prok prok prok 😀
Jumlah 10 suku pertama misal adalah
![S_n = \frac{n}{2}[2n + (n-1)b] S_n = \frac{n}{2}[2n + (n-1)b]](https://s0.wp.com/latex.php?latex=S_n+%3D+%5Cfrac%7Bn%7D%7B2%7D%5B2n+%2B+%28n-1%29b%5D&bg=ffffff&fg=000000&s=0)
![110 = \frac{10}{2}[2a + (10-1)b] 110 = \frac{10}{2}[2a + (10-1)b]](https://s0.wp.com/latex.php?latex=110+%3D+%5Cfrac%7B10%7D%7B2%7D%5B2a+%2B+%2810-1%29b%5D&bg=ffffff&fg=000000&s=0)
 ………(1)
………(1) dan
dan 


 ……..(2)
……..(2)


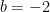
 , maka
, maka 

Jumlah dua suku berturut-turut berikutnya adalah -2, misal suku itu adalah
Dari persamaan (1) dan (2)
Jumlah dua suku pertama deret tersebut adalah
Thanks and good blog.
saya pernah dapet soal tentang deret seperti ini :
tentukan nilai dari deret :
5+1+8+5+11+9+ …. (sampai 80 suku)
sampai sekarang masih bingung tolong minta penjelasannya
terima kasih
Wah lumayan juga ya, saya akan coba memberikan gambaran deret tersebut.
5 + 1 + 8 + 5 + 11 + 9
Coba kita kurangkan suku kedua dengan suku pertama, suku ketiga dengan suku kedua, dan seterusnya.
1 – 5 = -4 (a)
8 – 1 = 7 (b)
5 – 8 = -3 (c)
11 – 5 = 6 (d)
9 – 11 = -2 (e)
Dari pola tersebut yaitu (a), (c), dan (e) selalu berurutan yaitu dari -4, -3, -2 dan terus naik.
Sedangkan (b) dan (d) juga berurutan yaitu 7, 6 dan terus turun.
Jadi mungkin suku berikutnya adalah sebagai berikut
5 + 1 + 8 + 5 + 11 + 9 + 14 + 13 + 17 + …..
Mungkin bisa memberikan inspirasi?
CMIIW
Ini gimana nih.. Huhuhu.. (bantu2 yaa)
“Biaya pembuatan sumur pd 1m pertama Rp10.000.000,- 1m kedua Rp13.000.000,- dan 1m strusnya brtambah Rp3.000,- dr bea sblmnya. Jumlah biaya yg dikeluarkan utk menggali sumur sdlm 10m adl …. ”
mksh sblmnya
Jadi, biaya untuk menggali sumur sedalam 10 meter adalah Rp37.000.000,00
kak, minta bantuannya donx…!!!
da soal : dik : U8 barisan aritmatika =15 sedangkan suku ke-2 dan suku ke-16 = 26
dit : a) cari suku pertama & beda
b) rumus untuk suku n..
mohon penjelasannya y kak….
mksh sblmnya… :’)
Barisan aritmatika ya, Oke
 ……. (1)
……. (1)
 ………. (2)
………. (2)



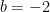 ke salah satu persamaan
ke salah satu persamaan



 dan
dan 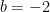
Substitusi dan eliminasi persamaan 1 dan 2
Substitusikan
Didapat
makasih banyak ya kak…. ^_^
Dik suatu barisan aritmatik dengan U3 U9 U11=75. Suku tengah =68 dan banyak sukunya 43, maka U43=… Mohon penjelasannya..
Dik suatu barisan aritmatik dengan U3 U9 U11=75.



Ini U3 + U9 + U1 = 75 atau bagaimana soalnya?
Dari persamaan (1) dan (2)


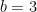

Jadi suku ke-43 adalah 131
suku kedua dan kedelapan dari suatu barisan geometri berturut” adalah 12 dan 768 suku kesepuluh barisan tersebut adalah
bantu dong kak..
masihh belum ngerti padahal hari senin mw ujian un ..
maksih kak.. 🙂
Diketahui barisan geometri.

 …………. (1)
…………. (1)
 …………. (2)
…………. (2)


 (kedua ruas dibagi 12)
(kedua ruas dibagi 12)
![r = \sqrt[6]{64} r = \sqrt[6]{64}](https://s0.wp.com/latex.php?latex=r+%3D+%5Csqrt%5B6%5D%7B64%7D&bg=ffffff&fg=000000&s=0)


Substitusikan persamaan (1) ke persamaan (2)
r = 2 disubstitusikan ke persamaan (1) untuk mencari nilai a, didapat a = 6
Semoga bisa membantu.
Bang, barisan dan deret itu bab di mata kuliah kapita selekta ya? teks book yang abang pake apa? mohon infonya,, pengin pinter juga kayak abang… 🙂
Barisan dan deret yang dimaksud di sini adalah untuk materi Matematika SMP/SMA 🙂