Garis singgung lingkaran merupakan garis yang memotong suatu lingkaran di satu titik dan tegak lurus dengan jari-jari di titik singgungnya. Pada dua buah lingkaran, terdapat garis singgung persekutuan dua lingkaran, yaitu garis singgung persekutuan dalam dan garis singgung persekutuan luar. Bagaimana cara menemukan rumus garis singgung persekutuan dalam dan garis singgung persekutuan luar dua lingkaran? Untuk menentukan panjang garis singgung persekutuan dua lingkaran tersebut, kita dapat menggunakan teorema pythagoras. Coba perhatikan berikut ini:
Garis Singgung Persekutuan Dalam

Pada gambar tersebut, terdapat dua buah lingkaran yang berpusat di P dan Q, dengan jari-jari R dan r. Garis p merupakan jarak titik pusat lingkaran PQ, sedangkan garis q merupakan garis singgung persekutuannya. Geser garis q melalui perpanjangan PA sejauh r sedemikian hingga terbentuk garis CQ dengan CQ//q. Perhatikan segitiga PQC siku-siku di C, dengan pythagoras maka:
karena CQ = q maka rumus panjang garis singgung persekutuan dalam adalah:
Keterangan:
q = garis singgung persekutuan dalam
p = jarak kedua titik pusat lingkaran
R, r = jari-jari lingkaran, dengan R > r
Garis Singgung Persekutuan Luar

Pada gambar tersebut, terdapat dua buah lingkaran yang berpusat di P dan Q, dengan jari-jari r dan R. Garis p merupakan jarak titik pusat lingkaran PQ, sedangkan garis l merupakan garis singgung persekutuan luarnya. Geser garis l sejauh r sedemikian hingga terbentuk garis PR dengan PR//l. Perhatikan segitiga PQR siku-siku di R, dengan pythagoras maka:
Karena PR = l, maka rumus panjang garis singgung persekutuan luarnya adalah:
Keterangan:
l = garis singgung persekutuan luar
p = jarak kedua titik pusat lingkaran
R, r = jari-jari lingkaran, dengan R > r

thank’s ia atas rumusnya.,.,. bisa tambah buat belajarr nih’ ‘ ‘ ‘ ‘
Iya sama-sama, moga bisa bermanfaat ya…
syukron akhi… tas ilmunya.. lok bisa gris singgung yang lain juga ya.. ellips, dan sbgnya tu..
Iya sama-sama mas, Insya Allah suatu saat kalau sempat saya buatkan postingan khususnya. Sering-sering saja mampir ke sini.
kak…
ad soal gini…
titik A,B dan C berada pada keliling lingkaran yang berpusat di P.
AC diameternya…
besar sudut BAC = X kuadrat…
sudut ACB = 3x kuadrat…
nilai x…???
Titik A, B, dan C pada keliling lingkaran, P sebagai pusat dengan AC = diameter.




Karena AC adalah diameter, maka
[Sudut keliling yang menghadap diameter besarnya 90°]
Jumlah sudut pada segitiga 90°
Apakah sudah cukup jelas?
iyya mkasih….
okok….
saya akan mapir ke sini terus…
ada lagi gini…
dua buag lingkaran O(3,5) dan M(1,5)
pamjang OM 13cm
panjang garis singgung persekutuan dalam adlah…
mohon bantuannya yy…
makasih….
Itu yang lingkaran O jari-jarinya 3,5 dan linkgaran M jari-jarinya 1,5? atau berupa koordinat cartesius?
koordinat cartesius kak….
Kalo koordinat kartesius kok gak ada jari-jarinya yah? cuma dikatakan jarak OM 13 cm. Kecuali ada keterangan kalo keliling lingkaran saling bersinggungan mungkin masih bisa dikerjakan. Kalo tidak ada jari-jarinya tidak bisa dikerjakan.
god job guys……….
thank you for your appreciation
wkwkwkwkwkw…..
toko ”hadi karya” memberikan diskon 25% untuk setiap barang yang di jual. sepasang sepatu di pasang Rp180.000,00. setelah di diskon, toko “hadi karya” masih memperoleh keuntungan 20% dari penjualan sepatu tersebut. harga pembelian sepasang tersebut adalah….
Sepasang sepatu dipasang Rp180.000,00 itu maksudnya dihargai atau dipasang harga atau gimana? Harga pembelian yang dimaksud itu pembelian oleh toko Hadi Karya atau harga pembelian oleh konsumen? Soalnya menurutku kurang jelas.





 maka:
maka:




Misalkan harga pembelian yang dilakukan oleh toko Hadi Karya adalah y, dan Rp180.000,00 adalah harga yang tertera di sepatu.
Misal harga pembelian adalah y, maka
Karena
Jadi, harga pembelian yang dilakukan oleh Toko Hadi Karya adalah Rp112.500,00
kurang paham saya pas yang di Y itu
Mudah-mudahan sekarang sudah paham, sering-sering saja mampir ke sini, OK?
Good job… Trima ksh bnyak yaaa….;-)
Oke, sama-sama. Moga bermanfaat…
Assalamu’alaikum
Dua buah lingkaran berpotongan di A dan B ; Jika P terletak pada lingkaran yang satu. Tarik PAC dan PAB serta C dan D terletak pada lingkaran yang kedua. Buktikan bahwa CD sejajar dengan garis singgung pada titik P ??????
Tolong dijawab ya dan dibikinkan gambarnya
terima kasih sebelumnya
Assalamu’alaikum
MAAF SALAH TULIS SOAL KA”
Dua buah lingkaran berpotongan di A dan B ; Jika P terletak pada lingkaran yang satu. Tarik PAC dan PBD serta C dan D terletak pada lingkaran yang kedua. Buktikan bahwa CD sejajar dengan garis singgung pada titik P ??????
Tolong dijawab ya dan dibikinkan gambarnya
terima kasih sebelumnya ka’
Walaikumsalam, maaf baru merespon. Soalnya sudah benar seperti itu? Tidak ada keterangan lain?
Saya baru membuat gambar animasinya, belum mempunyai solusi secara analisis.
Mungkin gambar animasi yang dibuat menggunakan geometer schecthpad ini bisa membantu, semua elemen yang ada bisa dianimasikan sehingga tahu perubahannya.
Silakan di donlot gambar+softwarenya, ukuran 1MB di link berikut.
soalnya seperti ini ka’
dua buah lingkaran berpotongan di A dan B; P terletak pada lingakaran yang satu. Tarik PAC dan PBD; C dan D terletak pada lingkaran yang kedua. Buktikan bahwa CD sejajar dengan garis singgung pada Titik P…
Alhamdulillah saya sudah ada aplikasi GEOGEBRA dan WINGEOM yang membahas tentang tersebut
tetapi saya binggung cara menggunakannya
saya sudah coba tetapi gagal
ada soal gni ,,,,,,,,,,,,,,,,
diberikan O(P,8cm) dan O(Q,15cm). berpotongan di C dan D . jarak sentral PQ=17cm. panjang busur CD adalah ……………..
Kak.. mau nanya.. aku ada soal..
Panjang jari-jari dua lingkaran 7 cm dan 3 cm. Jika panjang garis singgung persekutuan luarnya 15 cm, maka tentukan :
a. jarak kedua pusat lingkaran
b. panjang garis singgung persekutuan dalamnya.
a) Yang ditanyakan adalah jarak kedua pusat lingkaran, misal p





b) Gunakan rumus untuk mencari garis singgung persekutuan dalam





Kak Sholihin terima kasih atas bantuannya..
Jangan bosen ya kak.. kalo besok2 yunan nanya lagi..
Oke sama-sama, senang bisa membantu. Sering-sering aja mampir ke sini, follow twitter juga boleh.
saya mau taxa k”…
untuk membuktikan rumus persukutuan dua lingkaran gmn,,
1. persekutuan dalam lingkaran
2. persekutuan luar lingkaran
Untuk membuktikannya bisa memakai cara seperti di atas, memanfaatkan teorema phytagoras 🙂
kak mau nanya …………. aq ada soal gni kak
diberika O(P,8cm) dan O(Q,15cm). berpotongan di C dan D.jarak sentral PQ=17cm. panjang busur CD adalah ……………
Coba gambar 2 lingkaran yang berpotongan, berdasarkan keterangan soal maka nantinya akan terbentuk layang-layang PCQD, dengan PC adalah jari-jaring lingkaran P = 8 cm, QC adalah jari-jari lingkaran Q = 15 cm, dan PQ adalah jarang titik pusat P dan Q.


Pada layang-layang PCQD, perhatikan segitiga PCQ, dengan PC dan QC garis singgung, maka
diberika O(P,8cm) dan O(Q,15cm). berpotongan di C dan D. jarak sentral PQ=17cm. panjang garis busur CD adalah ……………….
wah makasih kak sholihin.. ini sangat membantu 😀
OK sama-sama, mudah-mudahan bisa bermanfaat. Jangan lupa share juga ya ke yang lainnya….
K pengen nanya kalo garis singgung persekutuan luar nya 20 ,garis antara kedua titik nya 25 ,dan salah satu jari jari dari kedua lingkarang ada lah 3 ..berapa jari jari lingkaran yang lain ..mohon di bantu
Misal garis singgung persekutuan luarnya l = 20





 maka
maka 
jarak antar 2 titik pusat p = 25
Karena
Jadi, jari-jari lingkaran yang lain adalah 18.
Makasih ..berarti aku salah waktu un haha ..makasi ya k
salam kenal, saya mau tanya dong. Kebetulan sekolah saya lagi banyak libur. jadi guru tidak sempat menjelaskan. saya cari di buku kebetulan entah mengapa tidak ada caranya di buku..
soal: Panjang jari2 dua lingkaran adalah 7cm dan 3cm. Jika panjang garis singgung persekutuan luarnya 15cm, maka tentukan jarak kedua pusat lingkaran!
Mohon bantuannya, terima kasih. 🙂
Namanya “saya” nih? mohon lain kali isikan data yang benar yah 🙂
 dengan R1 > R2
dengan R1 > R2




 cm
cm
Misalkan garis singgung persekutuan luarnya adalah l, dan jarak kedua titik pusat p, sedangkan jari-jari R1 dan R2.
Berdasarkan rumus garis singgung persekutuan luar dua buah lingkaran, maka:
Jadi, jarak kedua titik pusat lingkaran itu adalah
Ternyata soalnya sama dengan yang ditanyakan oleh Yunan, silakan dicari dikomentar sebelumnya.
iya kak, maaf saya baru lihat comen di atas setelah saya kirim pertanyaan itu.. hehe
Maaf kak nama saya Mukti.. bukan saya.. hehehee.. 😀
Nah gitu ada namanya kan enak manggilnya 🙂
Kalo soal ini..? sy bingung..
LINGKARAN A, B DAN C MASING-MASING BERJARI-JARI 6 CM DAN SALING BERSINGGUNGAN. DE DAN FG BERTURUT-TURUT MERUPAKAN GARIS SINGGUNG LINGKARAN A DENGAN C DAN B DENGAN C. DE DAN FG BERPOTONGAN DI TITIK H. PANJANG FH ?
Mohon bantuannya yaa,,
Kalau yang ditanya R1nya bagaimana rumusnya
Misal dari garis singgung persekutuan dalam



Untuk garis singgung persekutuan luar



Untuk keterangannya sama dengan yang sudah dijelaskan di atas.
Tapi ada kalanya dalam sebuah soal tidak dijelaskan mana yang lebih besar, kita hanya harus mencari jari-jari yang satu lagi. Nah di sinilah logika kita harus jalan 🙂
Semoga membantu.
Saya mau nanya
soal :
ditentukan jarak dua titik pusat lingkaran 20 cm . Panjang garis singgung persekutuan luarnya 16 cm . Panjang jari – jari lingkaran besar 15 cm . Hitungan panjang jari – jari lingkaran kecil .
Tolong di jawab
terima kasih
Misal jari-jari lingkaran besar adalah R, sedangkan jari-jari lingkaran kecil adalah r







 cm
cm
Rumus garis singgung persekutuan luar (l) dengan jarak antar pusat (p) adalah sebagai berikut:
Dari soal diketahui bahwa R = 15, maka:
Cara tersebut cocok untuk mengerjakan soal yang mirip tetapi tidak diketahui mana jari-jari lingkaran besar dan mana jari-jari lingkaran kecil. Hanya diketahui jari-jari salah satu lingkaran, maka cari jari-jari lingkaran lainnya.
Semoga membantu
maaf, aku mau nanya dong…
ini soalnya :
jarak antara pusat lingkran1 dgn lngkran2 adlah 30
jari-jari lingkaran1 adlah 16, sdgkan jari-jari lingkaran 2 adlah 4.. berapakah panjang garis singgung persekutuan luar ?
makasih sebelumnya 😀
Misal jarak antar dua pusat lingkaran adalah P = 30, sedangkan panjang garis singgung persekutuan luar misal l




 satuan panjang.
satuan panjang.
Jari-jari lingkaran 1 adalah R1 = 16, jari-jari lingkaran 2 R2 = 4. Berdasarkan rumus di atas, maka
Jadi, panjang garis singgung persekutuan luarnya adalah
ada 6 buah pipa yg d susun 2 berbanjar. dan pipa itu berdiameter 10 cm. tentukan panjang tali minimal yang dibutuhkan utnuk mengikat 6 pipa tersebut ?? tolong d jwab yh
Panjang Tali = 6 x diameter + Keliling lingkaran





Panjang tali yang dibutuhkan untuk mengikat susuan pipa tersebut sama dengan mencari diameter lingkaran ditambah dengan keliling lingkaran. Misal panjang tali adalah P, diamter pipa adalah D dan Keliling lingkaran adalah K
Jadi panjang tali minimal yang dibutuhkan untuk mengikat pipa tersebut adalah 91,4cm
bagaimana jika :
dua lingkaran berjari-jari 10cm dan 3cm , jarak kedua titik pusat nya 25cm. Panjang garis singgung persekutuan luar adalah?
mohon dijawab
sebab ini try out pertama 2012/2013
saya sulit mengerjakannya 🙂
Kan tinggal menerapkan rumus untuk mencari panjang garis singgung persekutuan luar seperti ulasan di atas 🙂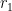 dan
dan 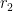 (dengan
(dengan  ) dan panjang garis singgung persekutuan luarnya adalah l. Maka:
) dan panjang garis singgung persekutuan luarnya adalah l. Maka:






Misalkan jarak kedua titik pusatnya adalah p, jari-jari lingkaran tersebut
Jadi, panjang garis singgung persekutuan luarnya adalah 24cm. Sulitnya di bagian mana nya?
Silakan kalau masih kurang jelas bisa ditanyakan lagi.
Aku mau nanya donk..
panjang jari-jari1 =9 cm dan jari-jari2 =4 cm. jika panjang garis singgung persekutuan luarnya 12 cm, tentukan
a. jarak kedua pusat lingkaran
makasih yaa,,
Diketahui r1 = 9cm; r2 = 4cm; l=12cm







Jadi, jarak pusat kedua lingkaran tersebut adalah 13cm.
kak aku amu izin bwt copy+paste artikelnya nih skaligus jga beberapa komentarnya. boleh gk kak?
Boleh saja, silakan semoga bisa bermanfaat. Mau dituliskan sumber refrensinya dari sini boleh, tidak dituliskan sumbernya juga tak apa. Yang penting untuk gambar silakan re-upload sendiri ya…
PQ merupakan garis singgung lingkaran. jika luas lingkaran 154cm2 dan panjang QR(sisi miring pada segitiga siku-siku)=18cm, panjang sisi datar segitiag tersebut………
a. 7 b. 18
c. 24 d.25
Pakai luas lingkaran untuk mencari jari-jari lingkaran tersebut (PR)



Berdasarkan teorema pytaghoras, maka:






kak.. pinter banget ya…
kakak kelas berapa ?
bls ya.. mksh
Kalo kaya gini gimanaa caranya yaaa?
Jarak kedua titik pusat 17cm dan panjang garis singgung persekutuan luarnya 15cm. Jika jari-jari salah satu lingkaran 25cm, maka jari-jari lingkaran satunya adalah…….
tolong dijawab yaaa makasiiii:)
Apakah soalnya sudah benar seperti itu? Jarak kedua pusat lingkaran 17cm, sedangkan salah satu lingkaran memiliki jari-jari 25cm. Ini berarti lingkaran yang 1 terletak di dalam lingkaran yang jari-jarinya 25cm.
minta tolong sebentar, kalo yang diketahui R1 nya 9 cm dan garis persekutuan luarnya 18 cari R2 nya gimana? minta tolong ya… makasih
Biasanya ada faktor lain yang diketahui, misal jarak kedua pusatnya. Misal diketahui jarak kedua pusatnya kan bisa dicari menggunakan rumus di atas 🙂
Untuk lebih jelas lagi silakan dibaca di komentar-komentar sebelumnya ya sudah dijelaskan
dua lingkaran masing-masing berjari-jari 12 cm dan 3 cm .berpusat di P dan Q. Jika panjang garis singgung persekutuan luarnya 12cm, maka jarak kedua pusat lingkaran tersebut adalah
Diketahui . Misal jarak kedua pusatnya adalah p maka:
. Misal jarak kedua pusatnya adalah p maka:






Jadi, jarak kedua pusat lingkaran tersebut adalah 15cm.
Semoga bisa membantu dan mudah dipahami.