Matematika SMA

Perbandingan Trigonometri Sudut-sudut Istimewa

Sholihin 14 April 2020 No Comments

Trigonometri dapat dikatakan sebagai suatu cabang ilmu matematika yang mempelajari mengenai sudut, sisi, dan perbandingan antara sudut terhadap sisi. Masih ingatkah dengan materi sebelumnya perbandingan trigonometri pada segitiga siku-siku? Untuk memudahkan menentukan perbandingan trigonometri pada segitiga siku-siku, dapat digunakan sindemi, cosami, tandesa, dan sebagainya.

Dalam trigonometri, ada istilah yang disebut dengan sudut istimewa, yang artinya adalah sudut-sudut yang nilai perbandingan trigonometrinya dapat ditentukan secara eksak, tanpa memakai kalkulator atau tabel matematika. Misalnya sudut 0°, 30°, 45°, 60°, dan 90° merupakan sudut-sudut istimewa di kuadran I. Untuk kuadran II, sudut istimewanya ada 120°, 135°, 150°, 180°. Sudut istimewa pada kuadran III ada 210°, 225°, 240°, dan 270°. Sedangkan di kuadran IV 300°, 315°, 330°, dan 360°.

Bagaimana cara menentukan nilai perbandingan trigonometri sudut-sudut istimewa tersebut? Untuk menentukan nilai perbandingan trigonometri pada sudut-sudut istimewa kita bisa menggunakan konsep yang sudah dipelajari pada perbandingan trigonometri utuk segitiga siku-siku. Berikut caranya.

Menentukan Perbandingan Trigonometri Sudut Istimewa

Perhatikan segitiga sama sisi ABC dengan panjang sisi 2 satuan berikut. Karena segitiga sama sisi, maka akibatnya ketiga sisinya sama dan ketiga sudutnya juga sama yaitu 60°.

Dari salah satu titik sudut, misal dari titik C, tarik garis tegak lurus CD ke sisi AB. Karena segitiga sama sisi, maka CD merupakan garis tinggi dan sekaligus garis bagi. Apa yang dimaksud dengan garis tinggi dan garis bagi? Pelajari pada materi Garis Istimewa pada segitiga.

Kita akan menentukan nilai perbandingan trigonometri untuk sudut 30° dan 60°. Pada segitiga sama sisi ABC di atas, kita akan memakai segitiga yang sebelah kana, yaitu segitiga BCD yang merupakan segitiga siku-siku.

Segitiga BCD

Dengan menggunakan terome pythagoras, kita bisa menentukan panjang CD. Perhatikan segitiga BCD! sisi BC merupakan sisi miring (hipotenusa).

CD=\sqrt{BC^2 - BD^2}=\sqrt{2^2-1^2}=\sqrt{4-1}=\sqrt{3}

Pada segitiga BCD, berlaku perbandingan trignometri berikut: (ingat perbandingan trigonometri pada segitiga siku-siku)

Trigonometri Sudut 30°

Nilai perbandingan trigonometri sudut 30° sebagai berikut:

\sin 30^\circ=\frac{BD}{BC}=\frac{1}{2}

\cos 30^\circ=\frac{CD}{BC}=\frac{\sqrt{3}}{2}=\frac{1}{2}\sqrt{3}

\tan 30^\circ=\frac{BD}{CD}=\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{3}=\frac{1}{3}\sqrt{3}

\csc 30^\circ=\frac{BC}{BD}=\frac{2}{1}=2

\sec 30^\circ=\frac{BC}{CD}=\frac{2}{\sqrt{3}}=\frac{2}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}}=\frac{2\sqrt{3}}{3}=\frac{2}{3}\sqrt{3}

\cot 30^\circ=\frac{CD}{BD}=\frac{\sqrt{3}}{1}=\sqrt{3}

Trigonometri Sudut 60°

Sedangkan untuk sudut 60°, nilai perbandingan trigonometrinya sebagai berikut:

\sin 60^\circ=\frac{CD}{BC}=\frac{\sqrt{3}}{2}=\frac{1}{2} \sqrt{3}

\cos 60^\circ=\frac{BD}{BC}=\frac{1}{2}

\tan 60^\circ=\frac{CD}{BD}=\frac{\sqrt{3}}{1}=\sqrt{3}

\csc 60^\circ=\frac{BC}{CD}=\frac{2}{\sqrt{3}}=\frac{2}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}} =\frac{2\sqrt{3}}{3}=\frac{2}{3}\sqrt{3}

\sec 60^\circ=\frac{BC}{BD}=\frac{2}{1}=2

\cot 60^\circ=\frac{BD}{CD}=\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{3}=\frac{1}{3}\sqrt{3}

Trigonometri Sudut 45°

Untuk menentukan perbandingan nilai trigonometri pada sudut 45°, perhatikan gambar berikut!

Segitiga PQR merupakan segitiga siku-siku sama kaki dengan panjang PQ = QR = 1 satuan. Maka panjang PR dapat ditentukan menggunakan teorema pythagoras.

PR=\sqrt{PQ^2+QR^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}

Maka perbandingan trigonometri untuk sudut 45° sebagai berikut:

\sin 45^\circ=\frac{PQ}{PR}=\frac{QR}{PR}=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1}{2}\sqrt{2}

\cos 45^\circ=\frac{QR}{PR}=\frac{PQ}{PR}=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{1}{2}\sqrt{2}

\tan 45^\circ=\frac{QR}{PQ}=\frac{PQ}{QR}=\frac{1}{1}=1

\csc 45^\circ=\frac{PR}{PQ}=\frac{PR}{QR}=\frac{\sqrt{2}}{1}=\sqrt{2}

\sec 45^\circ=\frac{PR}{QR}=\frac{PR}{PQ}=\frac{\sqrt{2}}{1}=\sqrt{2}

\cot 45^\circ=\frac{PQ}{QR}=\frac{QR}{PQ}=\frac{1}{1}=1

Secara lengkap, nilai perbandingan trigonometri sudut istimewa di kuadran I adalah sebagai berikut:

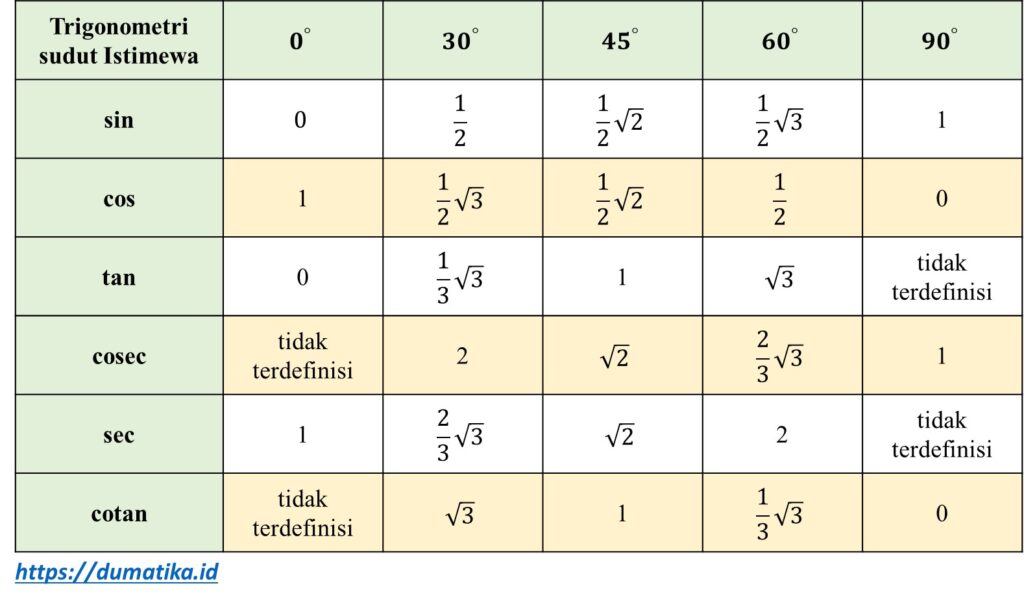
Perbandingan Trigonometri Sudut Istimewa

Contoh soal dan pembahasan perbandingan trigonometri sudut istimewa:

Tentukan hasil berikut!

  1. sin 30°
  2. sin 60° + cos 30°
  3. sin 45° + cos 45°
  4. tan 45°.cos 30°
  5. sin 30°.cos 45°.cot 90°

Pembahasan:

  1. sin 30° = 1/2
  2. \sin 60^\circ + \cos 30^\circ = \frac{1}{2}\sqrt{3} + \frac{1}{2}\sqrt{3}=\sqrt{3}
  3. \sin 45^\circ + \cos 45^\circ = \frac{1}{2}\sqrt{2}+\frac{1}{2}\sqrt{2}=\sqrt{2}
  4. \tan 45^\circ .\cos 30^\circ=1.\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}
  5. \sin 30^\circ .\cos45^\circ .\cot90^\circ =\frac{1}{2}.\frac{1}{2}\sqrt{2}.0=0

Contoh soal cerita

Sebuah tangga bersandar pada tembok. Jika sudut yang terbentuk antara kaki tangga dengan lantai adalah 30° dan panjang tangga 8 meter, maka tentukan ketinggian tembok!

Perhatikan ilustrasi gambar tersebut. Ketinggian tembok bisa kita tentukan dengan menggunakan trigonometri. Ketinggian tembok adalah AC.

\sin 30^\circ = \frac{AC}{BC}

\Leftrightarrow \frac{1}{2}=\frac{AC}{8} (ingat, sin 30° = 1/2)

\Leftrightarrow 2 \times AC = 1 \times 8 (perkalian silang)

\Leftrightarrow AC = \frac{8}{2} .

\Leftrightarrow AC=4

Jadi, ketinggian tembok yang dimaksud adalah 4 meter.

Untuk nilai trigonometri di kuadran lainnya, akan kita bahas setelah mempelajari sudut berelasi. Semoga bermanfaat, kalau ada yang kurang jelas bisa ditanyakan di kolom komentar.

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *